Statistical sampling analysis is most commonly used when one seeks to infer useful information about a relatively large population without examining every unit in the population by examining only a subset of that population (i.e. a sample). As part of sampling analysis, estimation or extrapolation is a procedure by which measured characteristics of a sample yield estimates, inferentially, about unknown characteristics of the population from which the sample was drawn …
In a simple example, one might select a sample of students from a school, measure characteristics of those students such as grade point average, and then use this data – inferentially – to estimate (i.e. extrapolate) grade point averages among all students at the school, in general. Sampling methodologies are described at-length in textbooks, journals and various industry guidelines, and are capable of producing useful results when properly applied. 
Probability Sampling
Only one type of sampling analysis, generally referred to as either probability sampling or statistical sampling, can appraise the results of a sample objectively. The term “probability” sample arises from the fact the sample is selected in a manner that is predictable in terms of the laws of probability, which eliminates both conscious and unconscious selection bias on the part of individuals performing sample selection. Such a sample must be obtained in a certain way (i.e. randomly), to be objective and defensible.
Samples obtained by any method other than random selection are generally considered to be “judgment” samples. Judgment samples typically result from haphazard selection or by means of convenience (i.e. choosing charts from the top of a pile). Consequently, when evaluating the conclusions of a judgment sample, “we must rely on the expert’s judgment – we cannot use the theory of probability. In contrast, the precision of an estimate made from a probability sample is never in doubt.”[1]
Forensus’ Framework of Sampling and Extrapolation
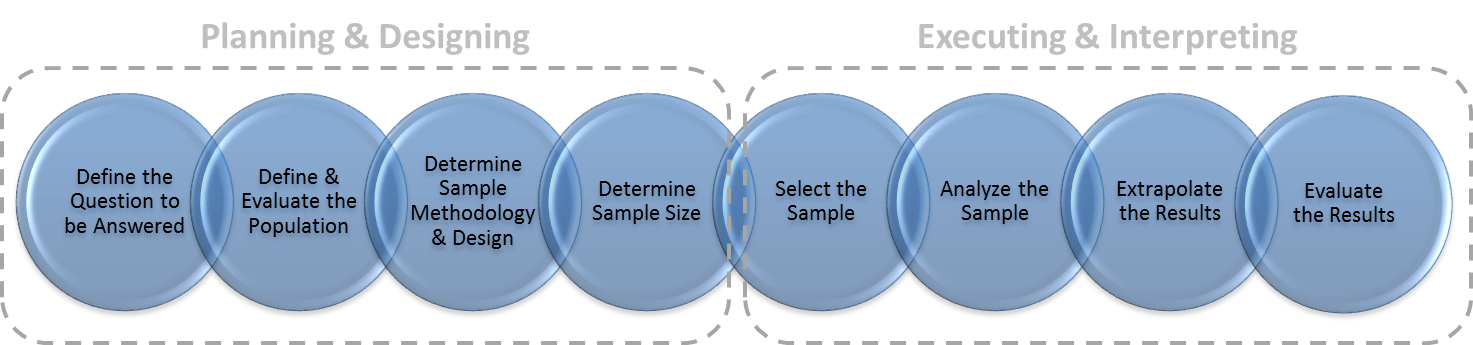
The major steps in the process of conducting sampling and extrapolation comprise a framework which will be discussed at length throughout this blog. This 8-step framework is comprised of: (1) defining the question to be answered; (2) defining the population, the sampling unit and the sampling frame; (3) designing the sampling plan; (4) determining the sample size; (5) selecting the sample; (6) reviewing each of the sampling units and analyzing their relevant characteristics; (7) estimating conclusions by extrapolating sample results; and finally (8) interpreting sampling conclusions to ensure they are useful and meaningful.
The first four steps of this framework comprise the planning and design phase of sampling, whereas the final four steps comprise the execution and interpretation phase. Together, these steps and phases are reflected in Figure 1. Our framework offers a standardized approach that can help to better achieve reliable results when conducting analysis. Sampling demands attention to all phases since poor work in one phase may render a study unreliable, even when everything else is done well.
Figure 1. Framework of Sampling and Extrapolation
Uncertainty of Sampling Conclusions
Unlike an examination of the entire population, which would typically yield definitive conclusions, sampling yields estimates about characteristics of the broader population along with a degree of uncertainty related to those estimates. This uncertainty exists due to the fact that only part of the population has been measured, and the magnitude of this uncertainty can be influenced by the methodology, techniques, assumptions and calculations used to perform the analysis. An estimate’s uncertainty is commonly described in terms of confidence and precision. Precision reflects the range of accuracy related to an estimated amount, while confidence is the degree of certainty that the sample correctly depicts the population. Together, confidence and precision yield a confidence interval, a range within which we estimate the true value of the population mean is likely to fall.
Conclusions based upon a sample, without consideration of the uncertainty surrounding the conclusions, are practically meaningless and there is no way to objectively know just how wrong they might be. Therefore, sampling conclusions should be considered in conjunction with their uncertainty to ensure they are useful for their desired purpose.
Conclusion
Statistical sampling and extrapolation is an increasingly common practice in healthcare compliance and litigation matters. Consequently, compliance officers, regulators and counsel should be aware of the techniques, strengths and limitations of using sampling for the purposes of estimating valid and meaningful conclusions. While the facts of any particular analysis may vary, robust and objective efforts to conduct analysis along with a firm grasp of the technical and practical implications of statistical sampling are best practices for reaching reliable and defensible conclusions.
statistical sampling
[1] Deming, W. Edwards, Sample Design in Business Research, New York: Wiley, 1990, p31.
This post was also published, in part, in the Society of Corporate Compliance and Ethics, SCCE Compliance and Ethics Blog
© Forensus Group, LLC | 2017

