Determining the sample size is an important step of planning a sample design. Too small a sample may diminish the utility and precision of the results, while too large a sample consumes excess time and effort …
However, common misconceptions exist in which it is believed a sample size must represent a large portion of the population, or that a sample’s size must be a fixed percentage of the total population (i.e. at least 10 or 20 percent). In fact, neither of these criteria is necessarily required to achieve valid conclusions. For example, a seemingly small sample can provide useful and valid conclusions if the sample is properly designed and executed. Recall that determining a sample size is Step Four of Forensus’ Sampling Framework:
Forensus’ Statistical Sampling Framework
Why Sample Size Matters
The determination of sample size by an analyst is decided largely by the nature of the sampling study and the level of error that is tolerable in its conclusions. Generally, increasing the size of the sample will reduce the level of random error (i.e. sampling error). Assuming all other steps of a study are properly executed, a general rule for sample sizes is “larger is better” with regard to a conclusion’s precision (i.e. with all else being equal, larger sample sizes generally provide conclusions with greater precision). Larger sample sizes are also more likely to be representative of the population.
Sample Size Considerations
A variety of practical considerations should be weighed when determining an acceptable sample size:
- The type of analysis being conducted (i.e. recall the question to be answered involves either continuous or discrete analysis);
- The particular sampling methodology (i.e. simple random, stratified, etc.);
- The degree of confidence and precision desired in the study’s conclusions;
- Past experience of the variability of possible analysis; and/or
- Any internal procedures, contractual obligations or statutory requirements establishing minimum sample size thresholds (i.e. OIG, CMS, etc.).
- For instance, the U.S. Department of Health and Human Services, Office of Inspector General (“OIG”), Provider Self Disclosure Protocol, dictates a minimum sample size of at least 100 sample units are required for self-disclosure purposes, whereas OIG’s Corporate Integrity Agreement FAQs does not stipulate a minimum size, but rather indicates a sufficient sample size should achieve conclusions attaining at least 90 percent confidence and 10 percent precision.
In addition to these practical considerations, a minimum sample size is required to satisfy the assumption of normality – a statistical assumption that, when satisfied, permits the use of certain equations to calculate and interpret sampling analysis. Sample sizes smaller than this amount may require non-parametric methods of analysis, thereby exceeding the technical expertise of many auditors, as well as the capabilities of basic software packages such as OIG’s RAT-STATS.
Based on these considerations, an appropriate sample size can be calculated using mathematical equations and/or the use of statistical software applications. These equations or applications can calculate a sample size expected to achieve a desired level of confidence and precision. For that reason, specifying the desired precision for estimates is an important part of sample design. The desired precision is the amount of sampling error that can be tolerated but that will still permit the results to be meaningful. In addition to specifying the desired precision of the estimate, analysts specify the degree of confidence that they want placed in that estimate. After completing the sampling analysis, the actual precision can then be calculated using the results of the sample.
The importance of defining a desired level of confidence and precision before selecting a sample cannot be overstated. In addition to enabling the analyst to perform calculations of sample size, there is also a more fundamental motivation. Establishing acceptance criteria (i.e. what conclusions will be deemed acceptable or not) prior to commencing analysis is a fundamental tenet of the scientific method. Determining the acceptable level of uncertainty after knowing the actual uncertainty may cloud an analyst’s objectivity, or worse, permit manipulation of a study’s conclusions. For instance, consider enrolling in a college course without knowing the criteria for earning an A, B, C, etc. Effectively, such a scenario allows the professor to assign grades at their discretion, with no regard for grading criteria – conducting sampling analysis without established acceptance criteria is similarly problematic.
Sample Size Calculator with RAT-STATS
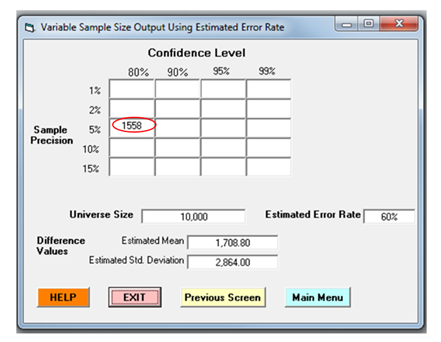
The figure below provides an example of the output from RAT-STATS’ sample size calculator, identifying a hypothetical sample size of 1,558 sampling units. Notably, this figure also identifies a variety of measurements involved in performing variable analysis sample size calculations, such as universe size, desired confidence and precision, estimated error rate, estimated mean and estimated standard deviation. In practice, many of these amounts are generally unknown, therefore techniques for estimating these amounts are required, such as evaluating a probe sample to provide reasonable estimates for these values. A probe sample is a preliminary sample evaluated to better-educate an analysts’ design of a statistical sample (read more about probe samples here). Alternatively, historical estimates of these measures may be useful.
Example RAT-STATS Sample Size Calculator Output
“Minimum Acceptable Sample Size”
A word of caution here – the mere fact that a sample was calculated using statistical formulas or software is not, in itself, a justification for the use of that sample size. Such calculations are based on the various inputs (i.e. desired precision, desired confidence, etc.). It is these considerations which must be evaluated when weighing the adequacy of a calculated sample size.
Notably, the concept of “minimum acceptable sample size” is often misunderstood by those executing and evaluating statistical analysis. The following are important considerations for determining an appropriate sample size and understanding its role in the conclusions:
- Although a sample may be of sufficient size to satisfy statistical requirements, it still may not be sufficient to achieve an acceptable level of precision and confidence. Said another way, basing a sample’s size on minimum technical benchmarks alone may not satisfy the real-world need for a more precise answer;
- Determining an appropriate sample size alone does not guarantee a study’s conclusions will be valid. The processes and procedures for planning and executing a sampling design should each be reasonable and appropriate, on their own, to provide a reasonable basis for valid conclusions. For example, an appropriate sample size selected without randomness, or selected from an ill-defined population may invalidate an analysis’ conclusions, even if an excessively large sample is reviewed; and
- While increasing the size of a sample will generally reduce the level of sampling error, the same cannot be said for non-sampling error. In other words, increasing the number of patients sampled cannot minimize the presence of non-sampling error. Therefore, analysts should address the risk of sampling error by meticulously planning and supervising the process of sampling analysis, while also employing a robust quality control program to mitigate the risk of data integrity and clerical errors.
Analysts should ensure each step of the sample size determination is properly documented, along with a record of all statistical software computations before proceeding to STEP FIVE of Forensus’ Sampling Framework: Selecting the Sample.
© Forensus Group, LLC | 2017